Distribución Binomial en Excel y Google Sheets
Este tutorial demostrará cómo trabajar con la Distribución Binomial en Excel y Google Sheets.
Descripción de la Función DISTR.BINOM
La Función DISTR.BINOM en Excel nos permite calcular dos cosas:
- La probabilidad de que ocurra un cierto número de resultados binarios (por ejemplo, la probabilidad de lanzar una moneda 10 veces, y que exactamente 7 de los intentos salgan cara).
- La probabilidad acumulada (por ejemplo, la probabilidad de que la moneda salga cara entre 0 y 7 veces).
¿Qué es la Distribución Binomial?
La distribución binomial abarca el rango de probabilidades de cualquier evento binario que se repite en el tiempo. Por ejemplo, digamos que se lanza una moneda justa 10 veces. Ciertamente, «esperas» que haya 5 caras y 5 cruz, pero aún así puedes terminar con 7 caras y 3 cruz. La distribución binomial nos permite medir las probabilidades exactas de estos diferentes sucesos, así como la distribución global de probabilidad para diferentes combinaciones.
La probabilidad de cualquier número individual de aciertos dentro de la distribución binomial (también conocida como ensayo de Bernoulli) es la siguiente:
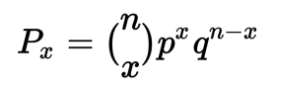
Donde:
n = el número de ensayos
x = el número de «éxitos»
p = la probabilidad de éxito de cualquier ensayo individual
q = la probabilidad de fracaso para cualquier ensayo individual, también denotada como 1-p.
Ejemplo de Distribución Binomial
En el ejemplo anterior, en el que se busca la probabilidad de sacar 7 de 10 caras en una moneda justa, se pueden introducir los siguientes valores
n = 10
x = 7
p = 0.5
q = 0.5
Después de resolver, se obtiene una probabilidad de 0,1172 (11,72%) de que exactamente 7 de las 10 tiradas salgan caras.
Ejemplos de Distribución Binomial en Excel
Para encontrar las probabilidades individuales y acumulativas en Excel, utilizaremos la función DISTR.BINOM en Excel. Usando el ejemplo anterior con 7 de 10 monedas que salen cara, la fórmula de Excel sería
=DISTR.BINOM(B3;C3;D3; FALSO)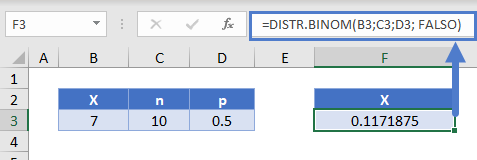
Donde:
- El primer argumento (7) es x
- el segundo argumento (10) es n
- El tercer argumento (0.5) es p
- El cuarto argumento (FALSO), si es VERDADERO, hace que Excel calcule la probabilidad acumulada para todos los valores menores o iguales a x.
Tabla y Gráfico de la Distribución Binomial
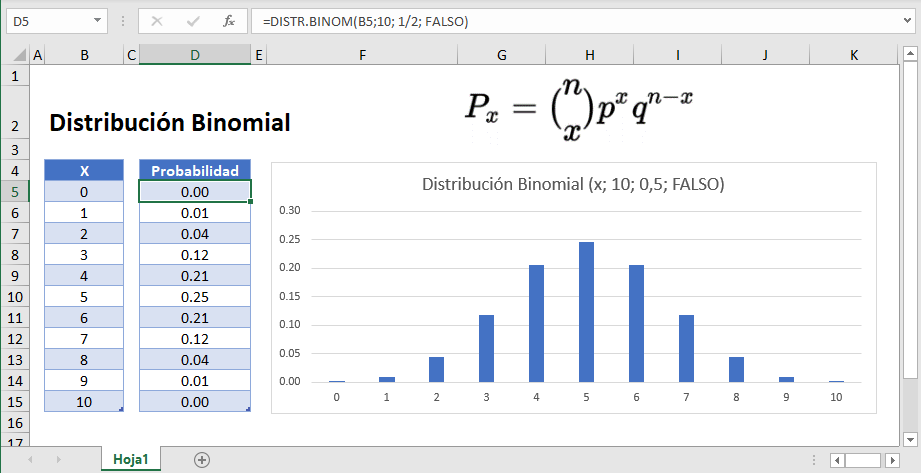
A continuación vamos a crear una tabla de distribución de probabilidad en Excel. La distribución de probabilidad calcula la probabilidad de cada número de ocurrencias.
=DISTR.BINOM(B10;10; 1/2; FALSO)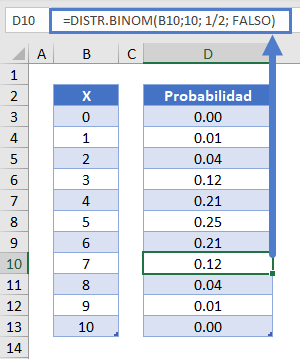
Leyendo esta tabla: hay aproximadamente un 12% de probabilidad de que exactamente 7 de 10 monedas salgan caras. Podemos crear un gráfico a partir de la tabla de distribución de la probabilidad binomial anterior.
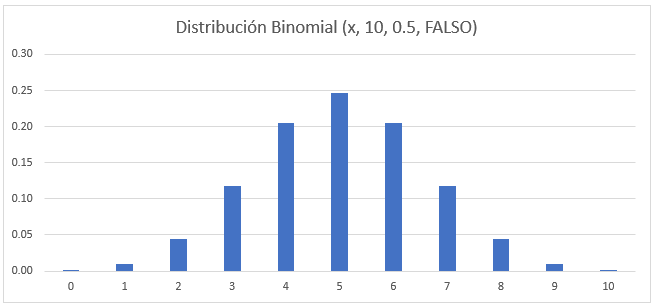
Gráfico de Distribución Binomial
Observa que la distribución binomial de este experimento tiene su pico en x=5. Esto se debe a que el número esperado de caras al lanzar una moneda justa 10 veces es 5.
Distribución de la Probabilidad Binomial Acumulada
Como alternativa, puedes optar por centrarte en la distribución de probabilidad acumulada. Ésta mide la probabilidad de un número de aciertos menor o igual a un número determinado.
En forma de gráfico, tiene el siguiente aspecto:
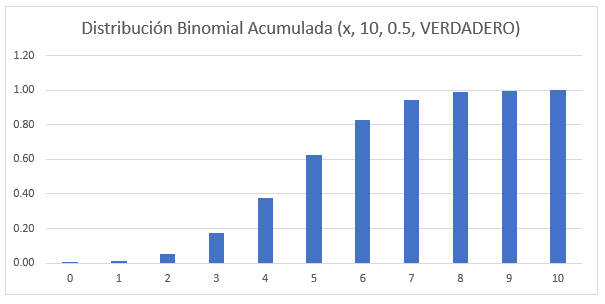
Para calcular la probabilidad acumulada, basta con sumar las probabilidades individuales calculadas en el apartado anterior. O puede utilizar la función DISTR.BINOM de la siguiente manera
=DISTR.BINOM(B10;10; 1/2; VERDADERO)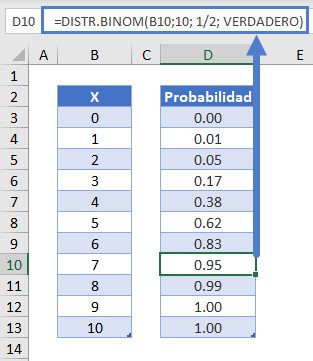
Observa que para calcular la probabilidad acumulada ponemos el último argumento en VERDADERO en lugar de FALSO. Matemáticamente, esta fórmula puede expresarse como sigue: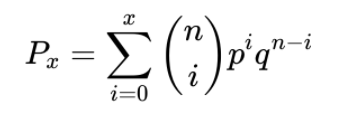 
DISTR.BINOM.SERIE – Encontrar la Probabilidad de un Rango de Valores
Mientras que DISTR.BINOM sirve para hallar la probabilidad de un único punto discreto, la función DISTR.BINOM.SERIE nos permite hallar la probabilidad de conseguir un determinado rango de aciertos. Utilizando el ejemplo de cara o cruz, podemos encontrar la probabilidad de que entre 6 y 8 de nuestros 10 intentos salgan cara con la siguiente fórmula.
=DISTR.BINOM.SERIE(10; 0.5; B9; C9)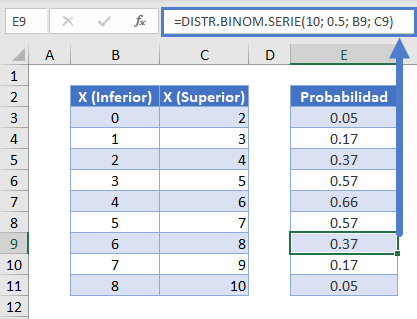
Valor Esperado Binomial – E(x)
Para una distribución binomial de n número de ensayos Bernoulli, podemos expresar el valor esperado para el número de aciertos: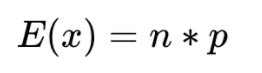 
Esto se puede calcular en Excel así
=B6*B6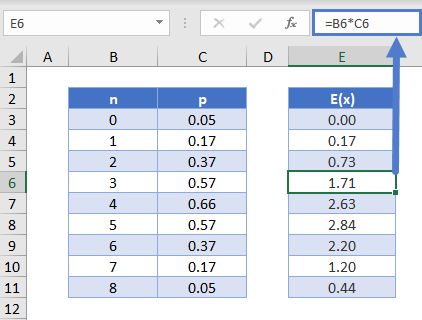
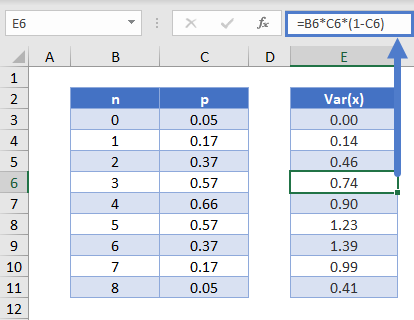
Varianza Binomial – Var(x)
Para calcular la varianza de la distribución, utilice la fórmula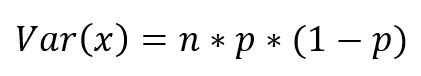 
Esto se puede calcular en Excel así
=B6*C6*(1-C6)
