Calculate Percent Variance in Excel & Google Sheets
Written by
Reviewed by
Download the example workbook
In this tutorial, we will learn how to calculate the percentage variance in Excel & Google Sheets.
Percent Variance
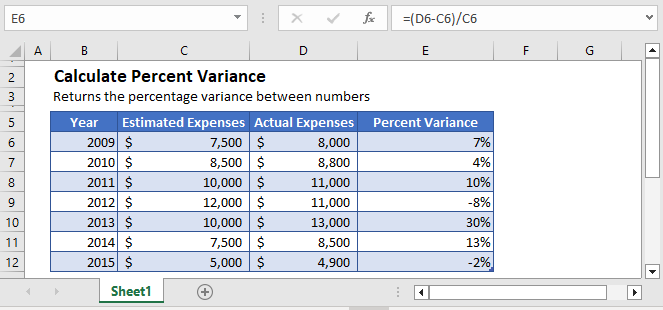
Percent variance shows the increase or decrease in an amount over time as a percentage of the total amount value.
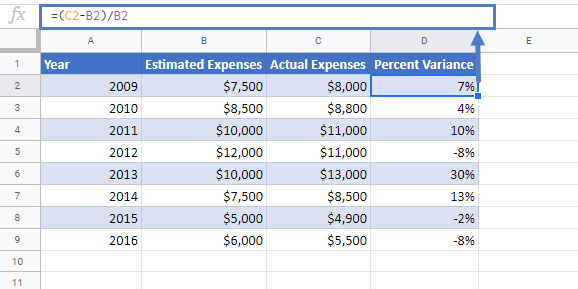
The percent variance between the two values is simply calculated by taking the difference between two values and dividing it with the old value.
=(new_value– old_value)/old_valueCalculate Year Over Year Variance
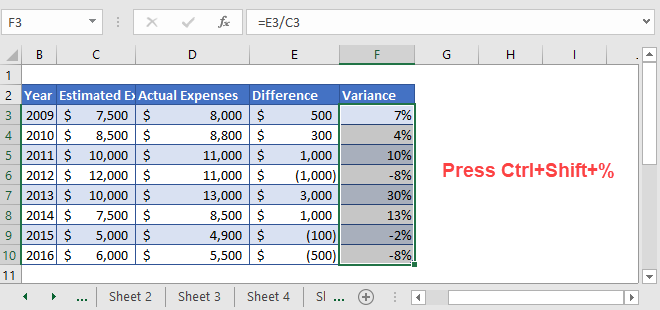
For example, you are required to do year over year analysis on the expenses data. You are given the estimated expenses and the actual expenses for that year and need to find out the year over year variance.
The year over year expenses variance can be calculated using the following formula:
=(D3-C3)/C3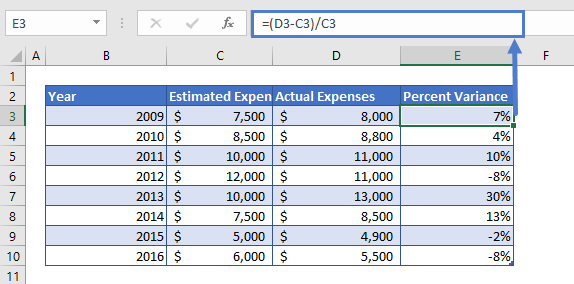
The formula can easily be understood by breaking it down into the following 4 steps:
Step 1
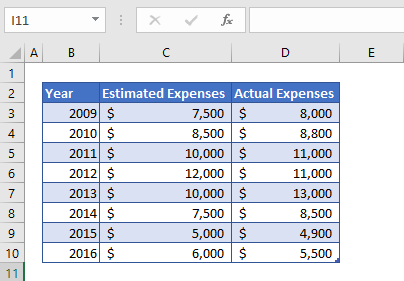
First of all, we need to prepare the data for the calculation of percent variance. Here, in the above table, we’ve put some values that we are going to use to find the percent variance between the estimated expenses and actual expenses.
Step 2
After preparing the data, we’ll calculate the difference between the values. The difference is simply calculated by subtracting the column D values from column C values.
=D3-C3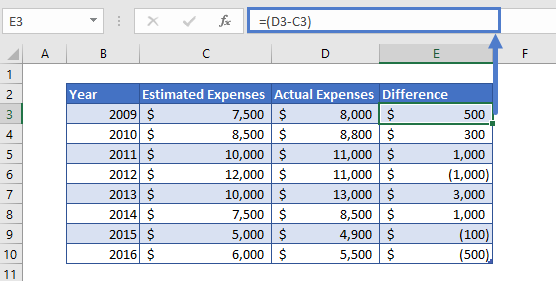
The difference we calculated can have a positive value or negative value, meaning the change in value can be positive and negative.
Step 3
Now we simply divide the difference value (Column D) with the Estimated Expenses (Column B). This will give us the result in number format
=E3/C3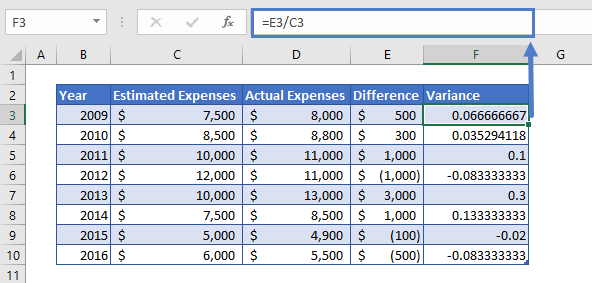
Step 4
The result we get in step 3 might be in number format. So, we’ll change the number format of the entire column F. To do so,
Select the entire column F and then press the shortcut key i.e. Ctrl+Shift+%.
Calculate Percentage variance in Google Sheets
This formula to calculate percent variance works exactly the same in Google Sheets as in Excel: