QUARTILE Function Examples – Excel, VBA, & Google Sheets

This tutorial demonstrates how to use the QUARTILE Function in Excel to calculate the quartile.

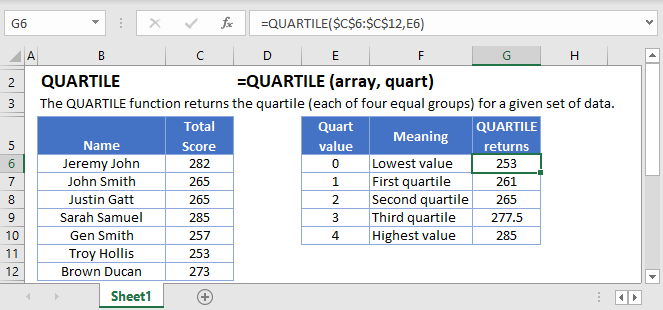
What is the QUARTILE Function?

QUARTILE is one of Excel’s statistical functions. It returns a quartile of range of data. You can specify whether you want the first, second, or third quartile. QUARTILE can also return the minimum and maximum values.

QUARTILE Is a “Compatibility” Function

As of Excel 2010, Microsoft replaced QUARTILE with two variations: QUARTILE.INC and QUARTILE. EXC.

QUARTILE still works, so if you have older spreadsheets using it, these will continue to work as normal. However, you should use QUARTILE.INC or QUARTILE.EXC wherever possible, just in case Microsoft drops QUARTILE from future versions of Excel.

What Is a Quartile?

Quartiles divide a range of data into four approximately even groups according to size. Excel calculates quartiles as percentiles:

• The first quartile is also known as the 25^th percentile – as 25% of the data is lower than this value.
• The second quartile is the median of the dataset, also known as the 50^th percentile as 50% of the data is lower than this.
• The third quartile is also called the 75^th percentile, as 75% of the data is lower than this value.

The quartiles, along with the smallest and largest numbers in the set, create the “five-number summary”. This can help you see at a glance where the middle of the data is, and how spread out it is.

How to Use the QUARTILE Function

Use QUARTILE like this:

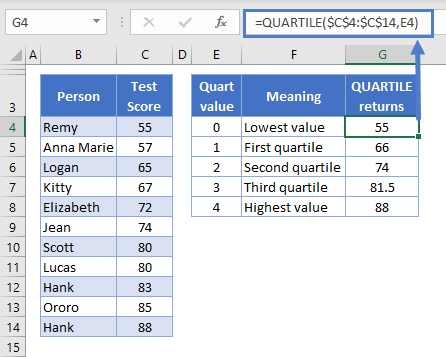
=QUARTILE(C4:C14,2)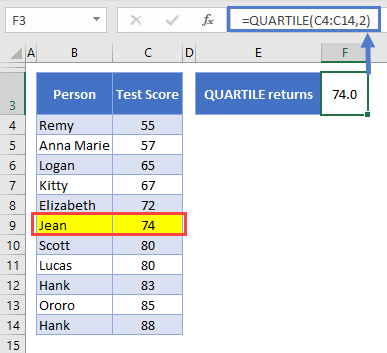

A group of students at an exclusive school have completed an important test. Their scores are stored in C4:C13, and data range this is the first argument we pass to QUARTILE.

The next argument in the function, which we refer to as “quart”, defines the value we want to return. Here we’ve chosen 2, the second quartile/median. The median is the middle number in the range, and as we have 11 students, the median is the 6^th one – Jean’s score of 74, which I’ve highlighted in the table.

A few handy things to know about QUARTILE:

• If quart isn’t a number, you’ll get a #VALUE! error
• If quart is less than 0 or greater than 4, you’ll get a #NUM! error
• If quart isn’t an integer, QUARTILE will ignore everything after the decimal point
• Blank or non-numerical cell in the data range are ignored
• If the data range is empty, you’ll get a #NUM! error

Creating the Five-Number Summary

When you define quart you have five options:

• 0 is the lowest number (equivalent to the Excel MIN Function<<link>>)
• 1 is the first quartile
• 2 is the second quartile (equivalent to the Excel MEDIAN Function<<link>>)
• 3 is the third quartile
• 4 is the largest value (equivalent to the Excel MAX Function<<link>>)

So if you want to create the five-number summary, you just create five QUARTILE functions, and change the quart value in each one. This is shown below:

QUARTILE.INC

As I mentioned earlier, Microsoft has replaced quartile with two functions – QUARTILE.INC and QUARTILE.EXC. QUARTILE.INC is exactly the same as QUARTILE. So if we switch these functions in our five-number summary table, we’ll get exactly the same results:

=QUARTILE.INC(C4:C14,E4)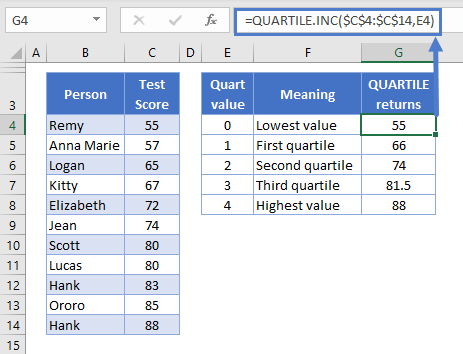

The “INC” part of the function is short for “inclusive”. This means that QUARTILE.INC includes the smallest and largest values in the data range when calculating the quartiles.

Excel calculates quartiles as percentiles: this can give slightly different results from the way quartiles are calculated in other analytical packages (typically by splitting the data into two halves, and calculating the median of each half).

Here’s how Excel calculates inclusive quartiles:

Location of Quartile  = (n - 1) * (target quartile / 100) + 1

Here n is the number of data points in the set. So let’s fill in the equation using the first quartile as an example:

Location of Q1 = (11 - 1) * (25 / 100) + 1

Our result = 3.5

This means the value of Q1 is the 3.5^th value, in other words, halfway between the third and fourth value.

To get the actual value we use the following:

Q1 = 3rd value + (4th value – 3rd value) * .5

Filling in the equation with our values:

Q1 = 65 + (67-65) * .5

Our result: 66

For a more in-depth discussion on how percentiles are calculated in Excel, see the main page on the Excel PERCENTILE Function<<link>>.

QUARTILE.EXC

QUARTILE.EXC is very similar to QUARTILE.INC, except that it excludes the smallest and largest values in the dataset when calculating the quartiles.

You use it like this:

=QUARTILE.EXC(C4:C14,2)

Here’s the same five-number summary calculated with QUARTILE.EXC:

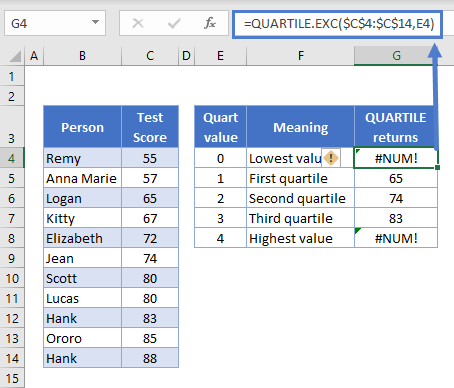
Well, the first thing that jumps out are the #NUM! errors when we set quart to 0 or 4. This is because, as mentioned earlier, QUARTILE.EXC excludes the smallest and largest values when creating its ranges. So you cannot create the five-number summary with QUARTILE.EXC.

Here’s how Excel calculates exclusive quartiles:

Location of Quartile  = (n + 1) * (target quartile / 100)

Let’s fill this in, again using the first quartile as our example:

Location of Q1 = (11 + 1) * (25 / 100)

Our result = 3

This means the value of Q1 is the 3rd value: Logan’s score of 65.

If we got a decimal in the result, that would indicate that the quartile falls between two values, and we’d get the value in the same way as with QUARTILE.INC:

Quartile = smallest value + (largest value – smallest value) * [the decimal from the first equation]

Again, for a more in-depth discussion on how percentiles are calculated in Excel, see the main page on the Excel PERCENTILE Function<<link>>.

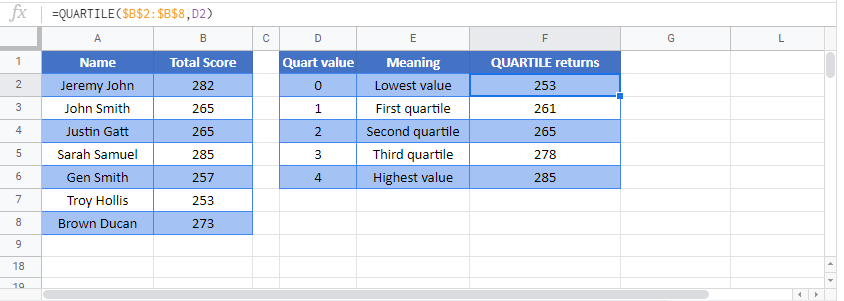
QUARTILE Function in Google Sheets

The QUARTILE Function works exactly the same in Google Sheets as in Excel:

QUARTILE Examples in VBA

You can also use the QUARTILE function in VBA. Type:

application.worksheetfunction.quartile(array,quart)