PERCENTILE Function Examples – Excel, VBA, & Google Sheets

This tutorial demonstrates how to use the PERCENTILE Function in Excel to calculate the percentile.

What Is the PERCENTILE Function?

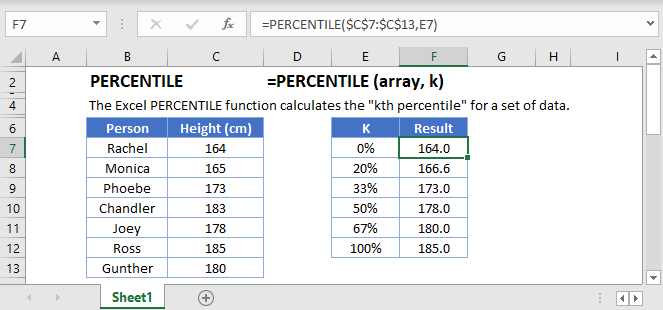
PERCENTILE is one of Excel’s statistical functions. It returns the k-th percentile of a given range of data.

PERCENTILE Is a “Compatibility” Function

As of Excel 2010, Microsoft replaced PERCENTILE with two variations: PERCENTILE.INC and PERCENTILE. EXC.

PERCENTILE still works, so older spreadsheets using it will continue to function as normal. However, if you don’t need your spreadsheet to remain compatible with older versions of Excel, you should use PERCENTILE.INC or PERCENTILE.EXC.

We’ll discuss all three so that you understand the ins-and-outs of each one.

What Is the Percentile?

The percentile tells you how a value compares to the other values in a given range. When a value is at the k-th percentile, this means that it is higher than k% of the other values in the group.

For example, if you’re a male living in the US and you’re 6ft (180cm) tall, you’re in the 71st percentile – you’re taller than 71% of other males in the US. If you’re female and 6ft (180cm) tall, you’re in the 99^th percentile – you’re taller than 99% of other females.

When you’re dealing with percentiles, note that the 50^th percentile is equal to the median of the data.

The Excel PERCENTILE Function tells you what the cut off point for a given percentile is – which is to say, how high a value needs to be in order to be in the k-th percentile.

How to Use the PERCENTILE Function

Use PERCENTILE like this:

=PERCENTILE(C4:C13,F3)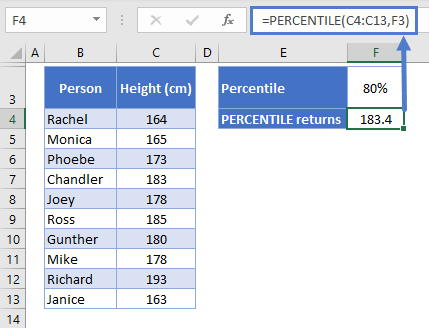

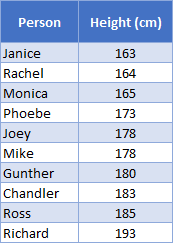
Here we have a few friends who have decided to calculate the 80^th percentile of the height of their group, and we see the result – 183.4cm.

The first argument in the function is the range of data – their heights, which we have laid out in C4:C13.

The next argument is the percentile. In this example, I’ve put the percentile in cell F3, and then referenced that cell in the function. This way, it’s easy to change the percentile and see the new results.

However, you can put the percentile directly into the formula if you want. You can define it as a decimal, like this:

=PERCENTILE(C4:C13,.8)

Or as a percentage, like this:

=PERCENTILE(C4:C13,80%)

And these all return the same value.

A few things to be aware of with PERCENTILE:

• If the percentile you define isn’t a number, the function will return a #VALUE! error
• If the percentile is less than 0 or greater than 1, you’ll get a #NUM! error
• Text and blank cells within your data range will be ignored

Two Methods of Calculating Percentiles

Let’s put our data in order for a second:

You might wonder why the 80^th percentile isn’t 183, since Chandler is the 8^th tallest person in the group.

Well, there are actually many ways to calculate the percentile mathematically, and no standardized or preferred method for all situations. This is something statisticians argue over in academic papers.

Excel gives you two ways of doing this, which brings us to PERCENTILE.INC and PERCENTILE.EXC.

PERCENTILE.INC

The Excel PERCENTILE.INC Function is the same as PERCENTILE. The “INC” part is short for inclusive, because it can calculate any valid percentile (that is, anything from 0% to 100%).

You use it like this:

=PERCENTILE.INC(C4:C13,F3)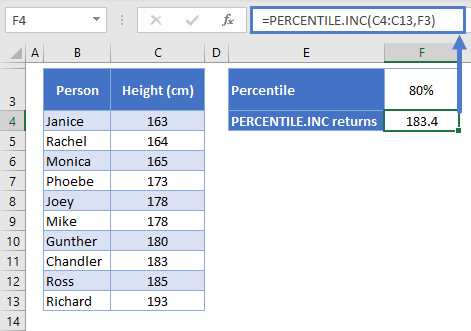

As you can see, it returns the same result that PERCENTILE did earlier.

So, going back to why the 80^th percentile isn’t exactly equal to Chandler’s height. Remember, we’re doing an inclusive calculation here, so we’re including all k values from 0 to 1 (or 0% to 100%).

This means that our shortest friend, Janice, is at the 0^th percentile, and Richard, the tallest, is the 100^th percentile. All the other friends are at equal increments between the two, and that increment is equal to 1/(n-1), where n is the number of data points in the range.

In our case, that’s:

1 / (10 – 1) = 11.111…

That means Chandler is not actually at the 80^th percentile, he’s at the 77.777^th percentile. If we plug that number into PERCENTILE.INC, we should get Chandler’s height…

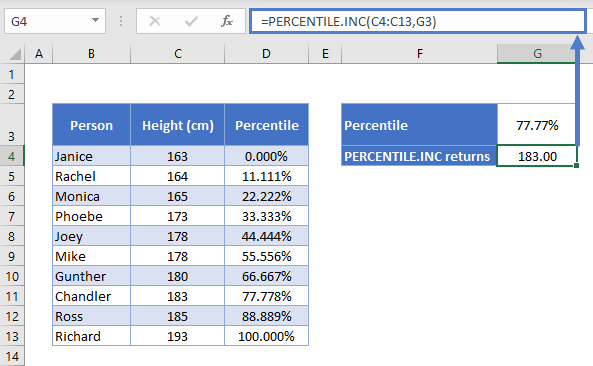
…and we do.

Linear Interpolation

Now, whenever the k value you specify is not a multiple of 1/(n-1), PERCENTILE.INC will apply a process called linear interpolation to calculate the result. This sounds complicated, but it basically means Excel will settle on a value between the two.

So why did we get 183.4 when we asked for the 80^th percentile earlier?

The calculation works as follows:

• The 80^th percentile falls between Chandler and Ross, Chandler at the 77.777^th percentile, and Ross at the 88.888th.
• The 80^th percentile is 2.222% ahead Chandler’s height
• We know there’s an 11% distance between Chandler and Ross’ heights
• 222% / 11.111% = 20% after rounding. Now we know that the 80^th percentile is 20% of the way between Ross and Chandler’s heights.
• The difference between Ross’ height of 185cm, and Chandler’s height of 183cm, is 2cm
• 20% of 2cm is 0.4cm
• Add that on to Chandler’s height, and we get 183.4cm

PERCENTILE.EXC

You use PERCENTILE.EXC in essentially the same way:

=PERCENTILE.EXC(C4:C13,F3)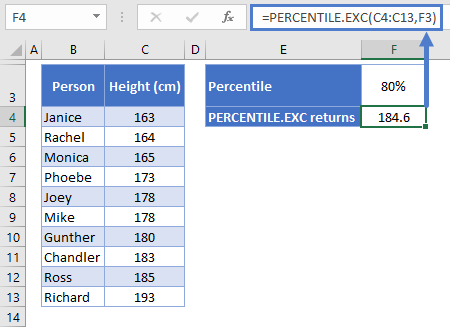

Okay, so we’ve got the same data, we want the same percentile, but we got different results. Why is that?

It’s because PERCENTILE.EXC excludes the first and last values when calculating its percentile intervals. See below:

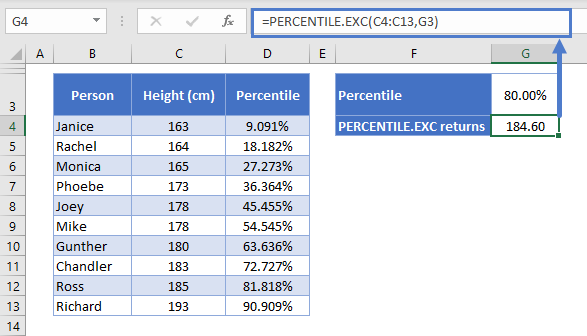
Rather than the interval being equal to 1/(n-1), with PERCENTILE.EXC the interval is 1/(n+1), or in this case, 9.091%.

Everything else works the same way as with PERCENTILE.INC. Again, the 80^th percentile is between Chandler and Ross, so Excel applies the same method of linear interpolation:

• The 80^th percentile falls between Chandler and Ross, Chandler at the 72.727^th percentile, and Ross at the 81.818th.
• The 80^th percentile is 7.272% ahead Chandler’s height
• We know there’s an 9.091% distance between Chandler and Ross’ heights
• 272% / 9.091% = 80% after rounding. Now we know that the 80^th percentile is 80% of the way between Ross and Chandler’s heights.
• The difference between Ross’ height of 185cm, and Chandler’s height of 183cm, is 2cm
• 80% of 2cm is 1.6cm
• Add that on to Chandler’s height, and we get 184.6cm

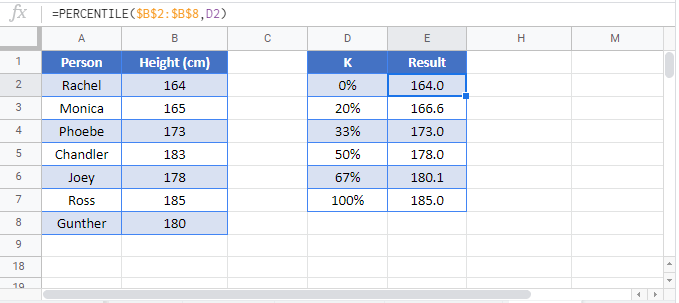
PERCENTILE in Google Sheets

The PERCENTILE Function works exactly the same in Google Sheets as in Excel:

PERCENTILE Examples in VBA

You can also use the PERCENTILE function in VBA. Type:

application.worksheetfunction.percentile(array,k)